从CPU RTL到GCC expmed Cost Model
背景
最近和朋友讨论一个编码算法的问题的时候意外发现,当前 RISC-V 的 GCC 即使使用-O3优化的情况下,也不会将 divide by const 优化为Barrett reduction。但我测试了默认参数的 x86 、 aarch64 、 mips32 ,均存在该优化。且通常来说, CPU 的乘法器实现的最长 Latency 会小于除法器的实现,在许多微架构中甚至是远小于,因此这个优化在许多情况下是十分有必要的。
由此,这个问题成功引起了我的兴趣,经过几天的摸索大概看懂了 gcc 处理 expmed Cost Model 的代码,并找到了问题的根源。
现象
int div6(int x) {
return x / 6;
}
int div4(int x) {
return x / 4;
}
int div998244353(int x) {
return x / 998244353;
}https://godbolt.org/z/EPT3Wz634
然后分别使用 gcc 13.2.0 与 llvm 16.0 使用-O3进行编译,分别得到以下 asm :
gcc 13.2.0:
div6(int):
li a5,6
divw a0,a0,a5
ret
div4(int):
sraiw a5,a0,31
srliw a5,a5,30
addw a0,a5,a0
sraiw a0,a0,2
ret
div998244353(int):
li a5,998244352
addiw a5,a5,1
divw a0,a0,a5
retllvm 16.0:
div6(int): # @div6(int)
lui a1, 174763
addiw a1, a1, -1365
mul a0, a0, a1
srli a1, a0, 63
srli a0, a0, 32
addw a0, a0, a1
ret
div4(int): # @div4(int)
slli a1, a0, 1
srli a1, a1, 62
add a0, a0, a1
sraiw a0, a0, 2
ret
div998244353(int): # @div998244353(int)
lui a1, 70493
addiw a1, a1, -2031
mul a0, a0, a1
srli a1, a0, 63
srai a0, a0, 58
add a0, a0, a1
ret由此看出, llvm 会正确地将常数除法优化为Barrett reduction,但 gcc 只考虑了优化 2 的整数幂为运算符右移。
但令人不解的是,我测试了其他主流的 isa ,包括 x86 、 aarch64 、 mips32,均不存在该现象,由此便开始从 gcc 的代码一探究竟。
找到 gcc 代码中处理运算符替换的函数
对于 gcc 如此大的一个编译器来说,快速定位实现某个功能的函数位置可能难以使用搜索引擎得到,尤其是这种很少人关注的部分。
那么,我们可以问问神奇的AI:
而在GCC的expmed.cc,注释中写着:
/* Medium-level subroutines: convert bit-field store and extract
and shifts, multiplies and divides to rtl instructions.
Copyright (C) 1987-2023 Free Software Foundation, Inc.经过对 gcc 这部分源代码以及注释的阅读,我确信 AI 没有骗我,便开始了通过 gdb 单步执行阅读代码的过程。
调试
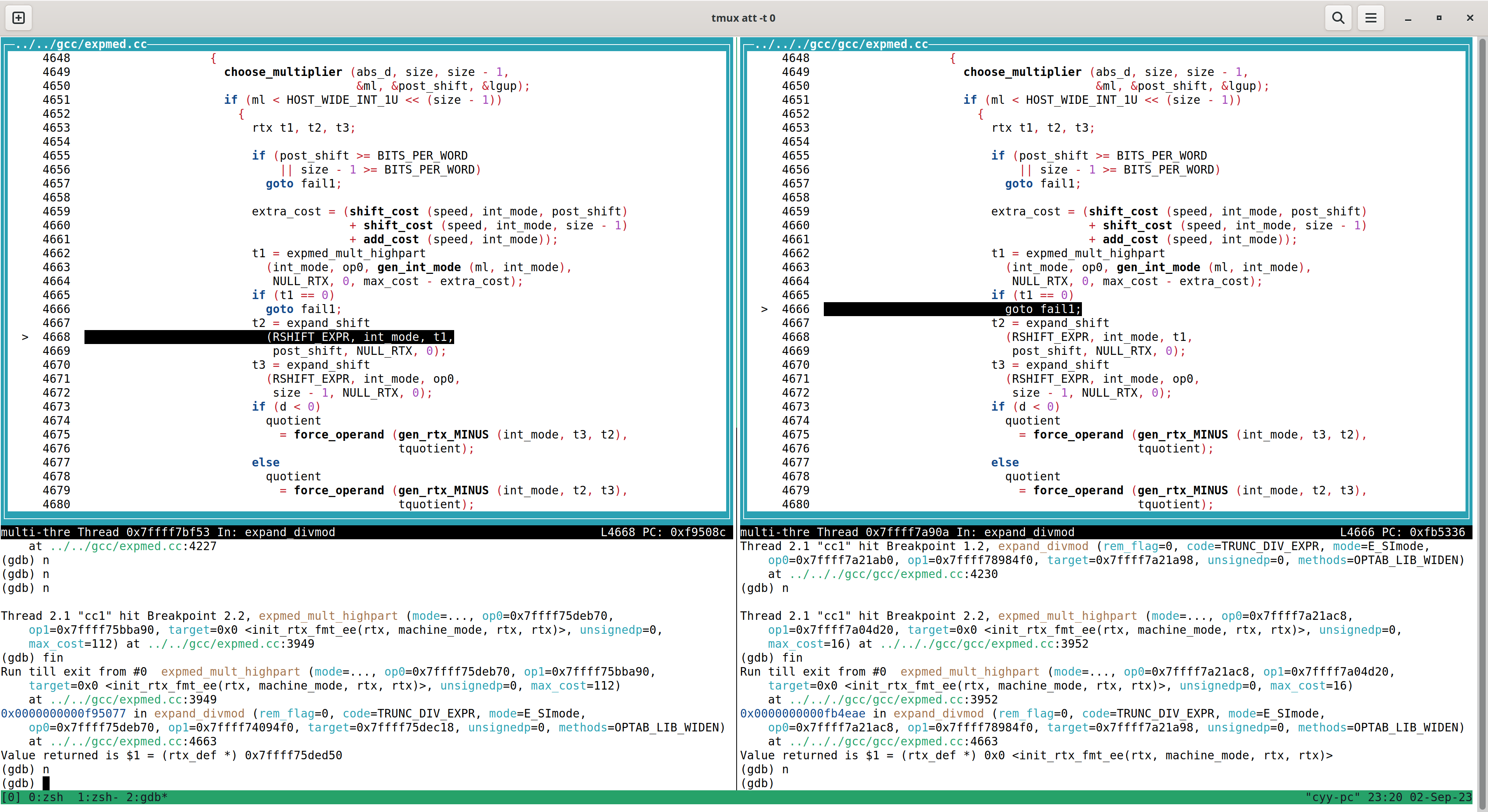
于是,我将 gcc 仓库拉下来(我git checkout到了860b0f0ef787f756c0e293671b4c4622dff63a79,也就是2023年8月1日的gcc 13.2.1),然后使用-O0 -g选项分别编译了 x86 与 RISC-V 的 gcc,然后使用 gdb 对 gcc 进行调试,在expand_divmod函数处打断点,然后一步步 next 单步执行,每次对比 x86 与 RISC-V 的 GCC 的执行过程,果然发现了端倪。
我将上面的代码保存为1.c,然后使用以下 .gdbinit 来控制 risc-v gcc ,对于 x86 gcc 也是类似:
add-symbol-file /home/cyy/tmp/riscv-gnu-toolchain/build-gcc-linux-stage1/gcc/expmed.o
add-symbol-file /home/cyy/tmp/riscv-gnu-toolchain/build-gcc-linux-stage1/gcc/riscv.o
b expand_divmod
set follow-fork-mode child
layout src
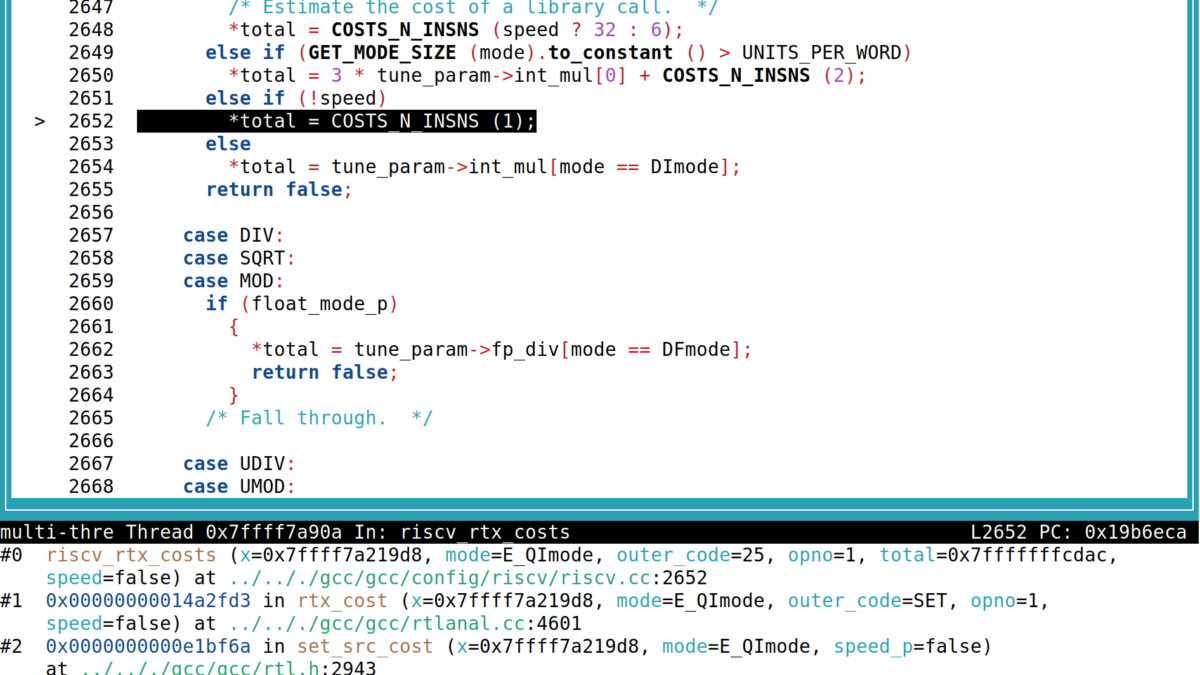
r -S -O3 1.c图中,左为 x86 的 gcc ,右边为 risc-v 的 gcc ,我们发现,右边x86的gcc在4662行调用expmed_mult_highpart后,返回值非0,继而没有选择goto fail1分支,而risc-v却选择了goto fail1,由此导致gcc不再尝试进行更多的优化。
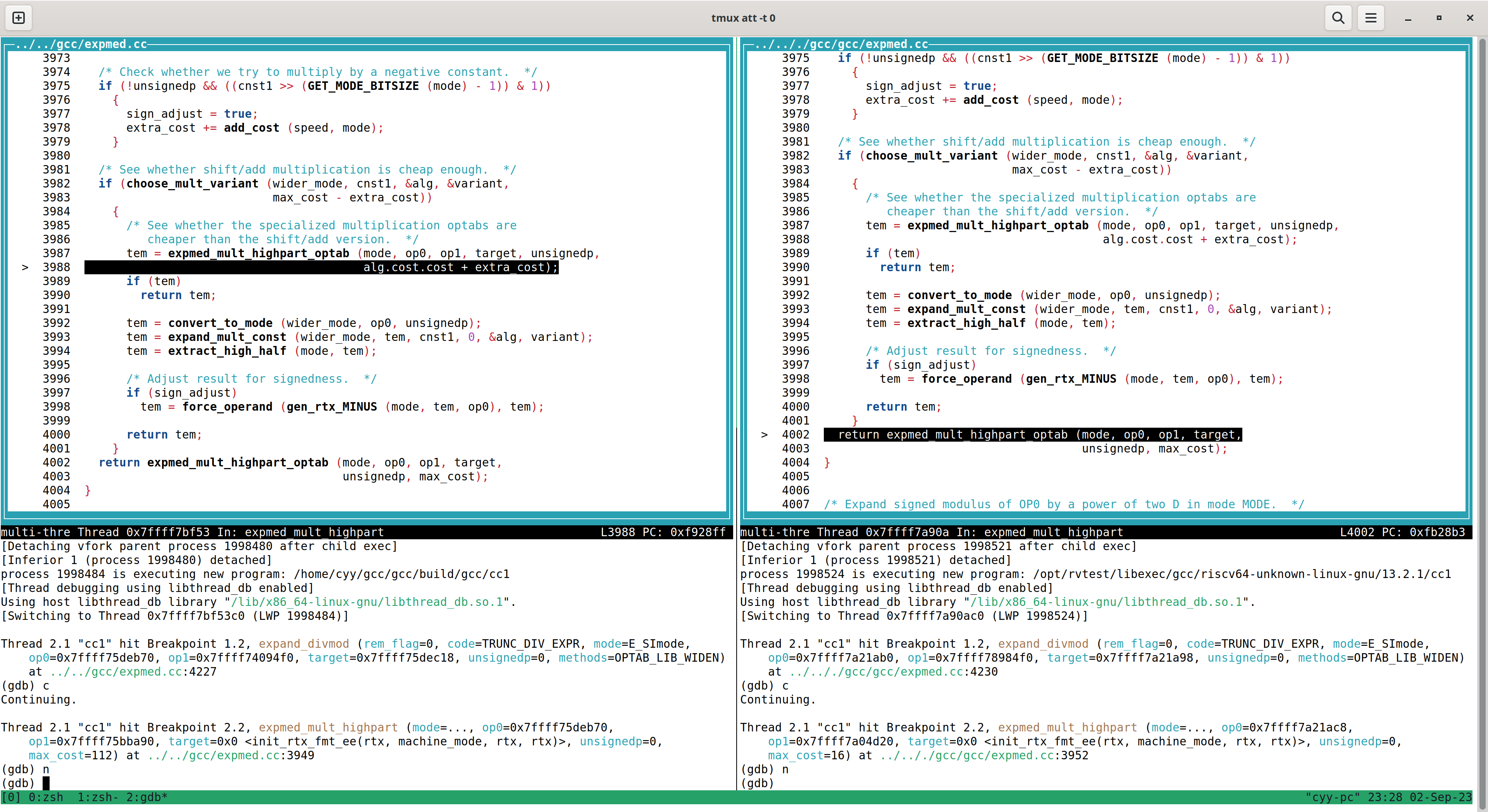
那既然是这个函数产生了不同,我们就step进入这个函数看看里面发生了什么,于是我添加这个函数为断点重新运行程序:
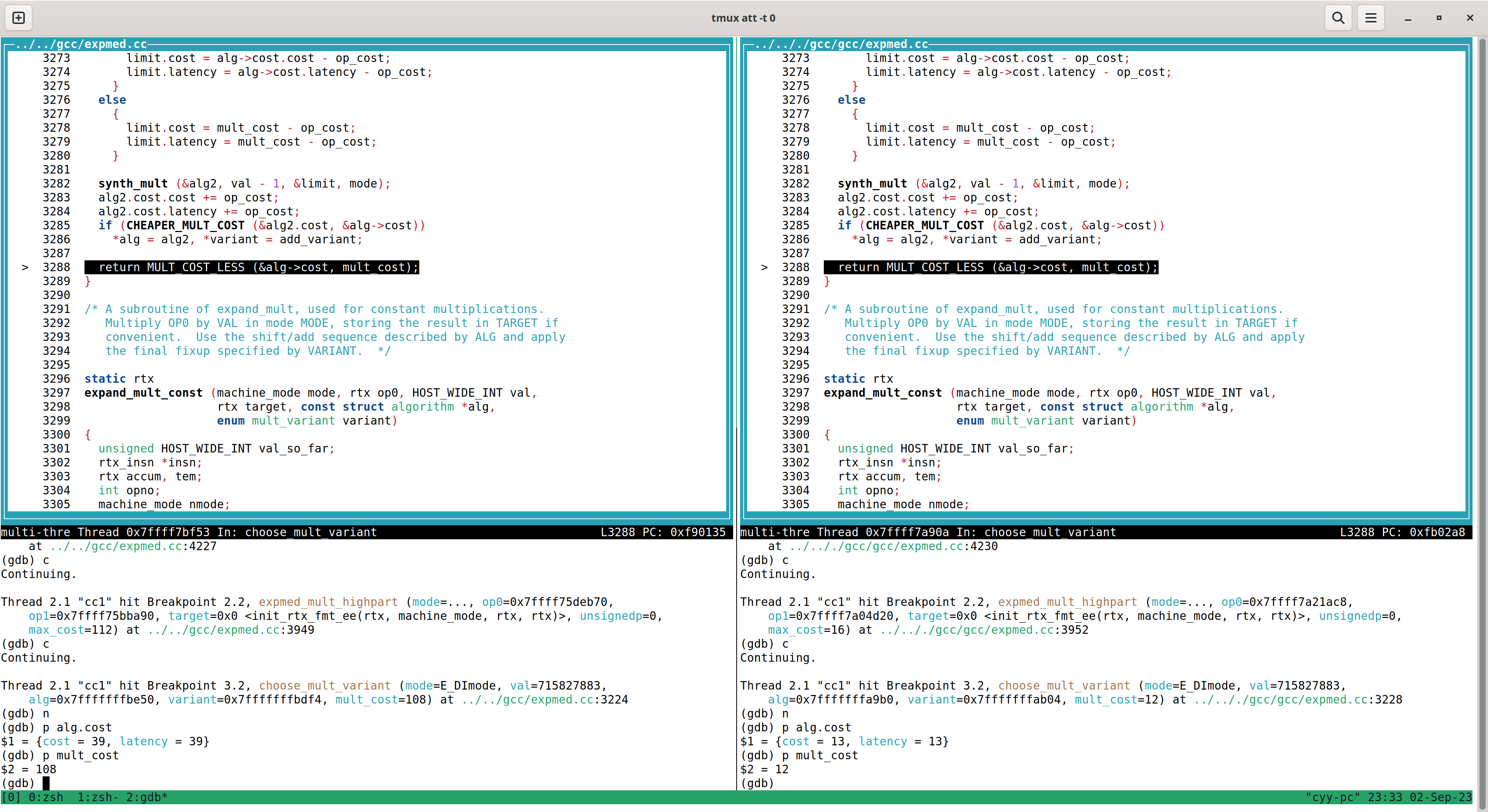
结果又发现了控制流的不同,在choose_mult_variant返回后产生了不同的控制流,那么同样,再次添加断点,重新运行程序:
尽管上面控制流略有不同,但该函数的最终返回值来源于MULT_COST_LESS宏,于是我先 print 了一下他们的值,然后观察了一下该宏的代码:
/* This macro is used to compare a pointer to a mult_cost against an
single integer "rtx_cost" value. This is equivalent to the macro
CHEAPER_MULT_COST(X,Z) where Z = {Y,Y}. */
#define MULT_COST_LESS(X,Y) ((X)->cost < (Y) \
|| ((X)->cost == (Y) && (X)->latency < (Y)))由此看出, x86 与 riscv 两边因为 cost 大小关系不同,产生了不同的 MULT_COST_LESS 的结果。
那么问题又来了,这里用的 cost 又从何而来,为什么会出现这样的值。
在gdb中使用bt观察调用栈,然后一层层up,最后发现,mult_cost来源于expand_divmod的max_cost值,对应代码如下:
/* Only deduct something for a REM if the last divide done was
for a different constant. Then set the constant of the last
divide. */
max_cost = (unsignedp
? udiv_cost (speed, compute_mode)
: sdiv_cost (speed, compute_mode));然后观察udiv_cost与sdiv_cost,所处的文件,发现:
这里有 set_mul_cost、set_sdiv_cost、set_udiv_cost,我们直接看在哪会调用这些函数:
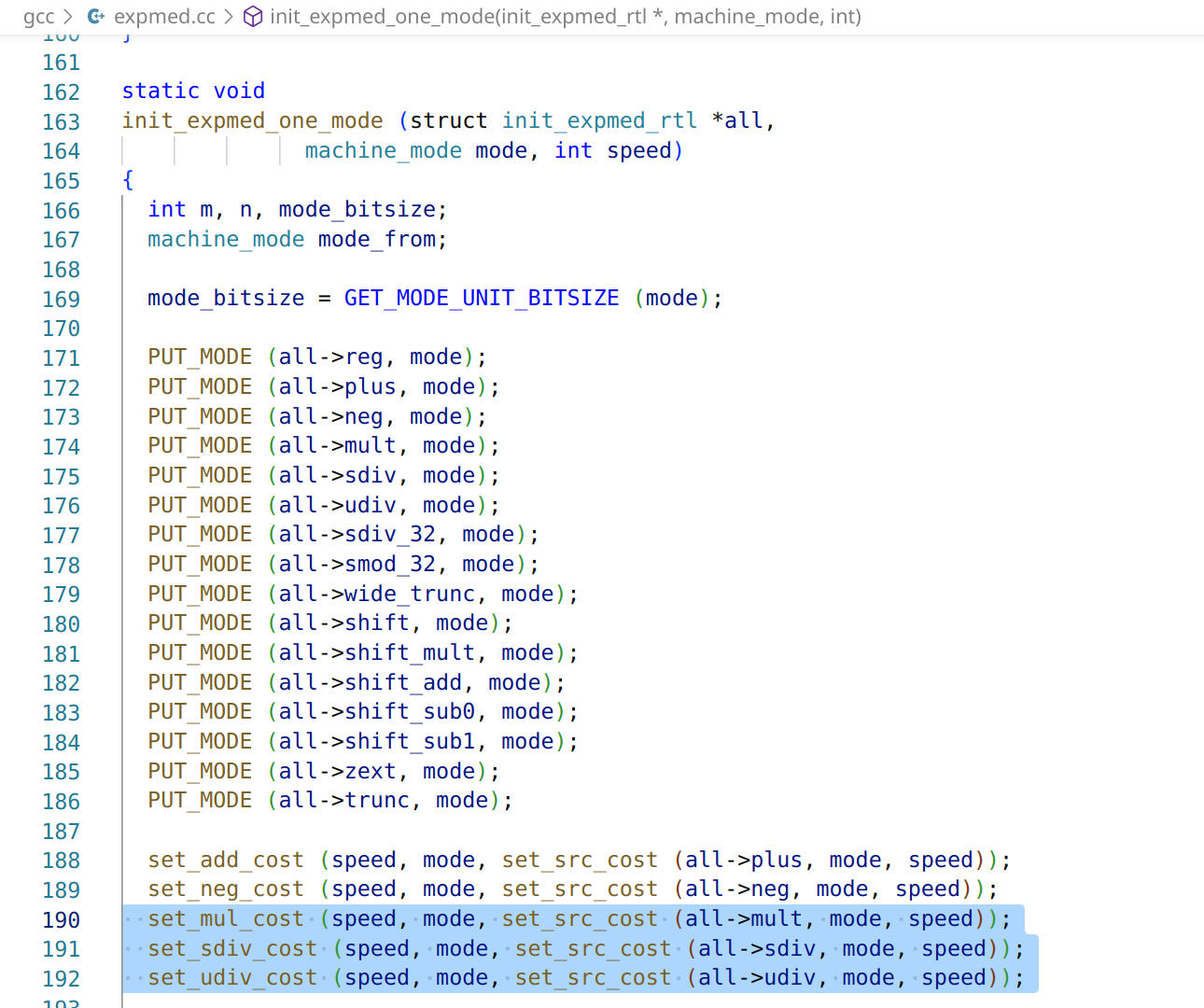
接着,我们再对init_expmed_one_mode添加断点,看看它在哪被调用:
可以看到,在上一层的init_expmed会枚举所有的参数,包括了所有mode,以及是否speed模式。
至此,已经了解了gcc初始化expmed的过程,现在我们来看cost的计算。
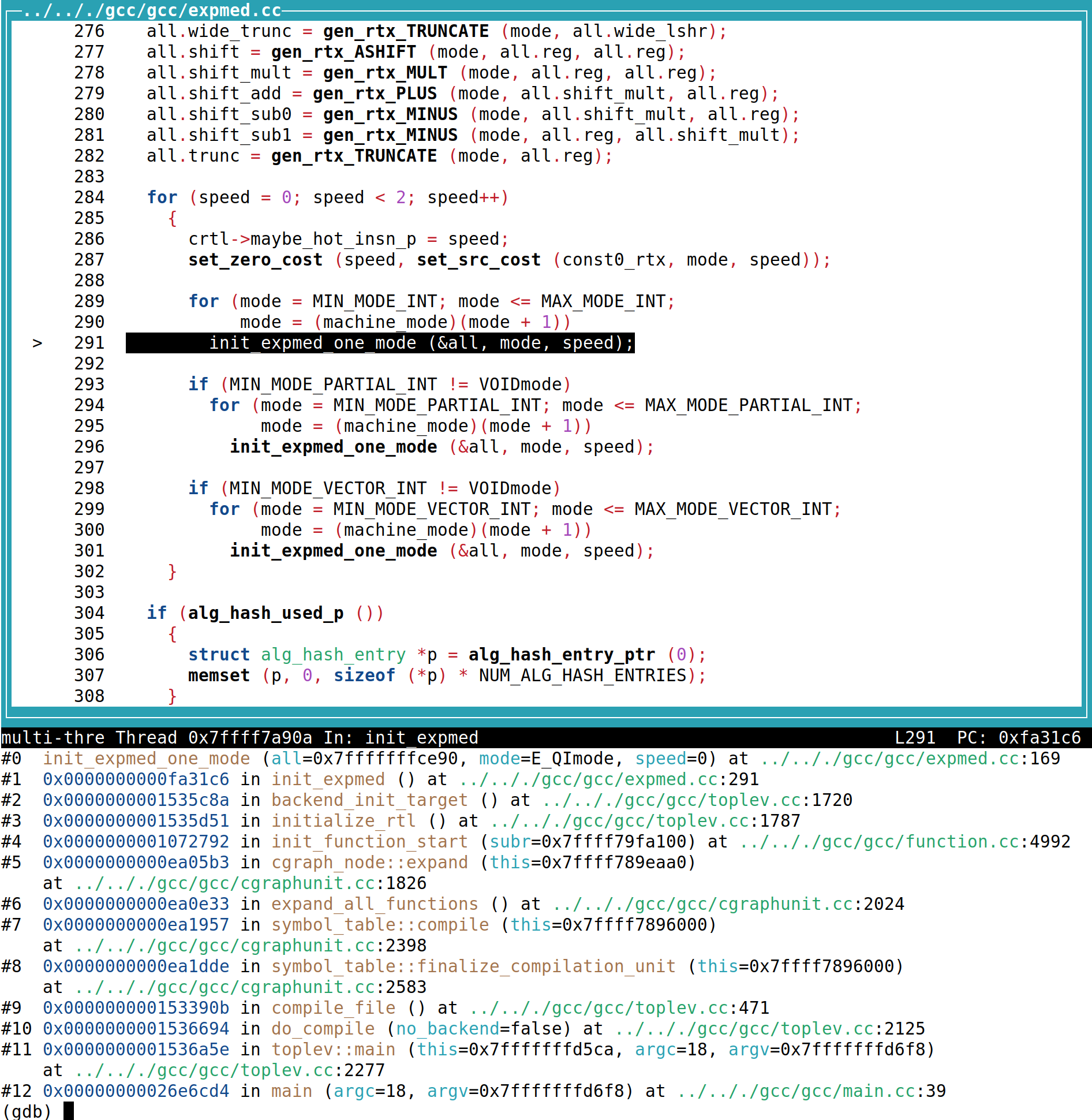
因此,我选择清除init_expmed_one_mode的断点,但保留set_mul_cost、set_sdiv_cost、set_udiv_cost的断点,再次运行程序。
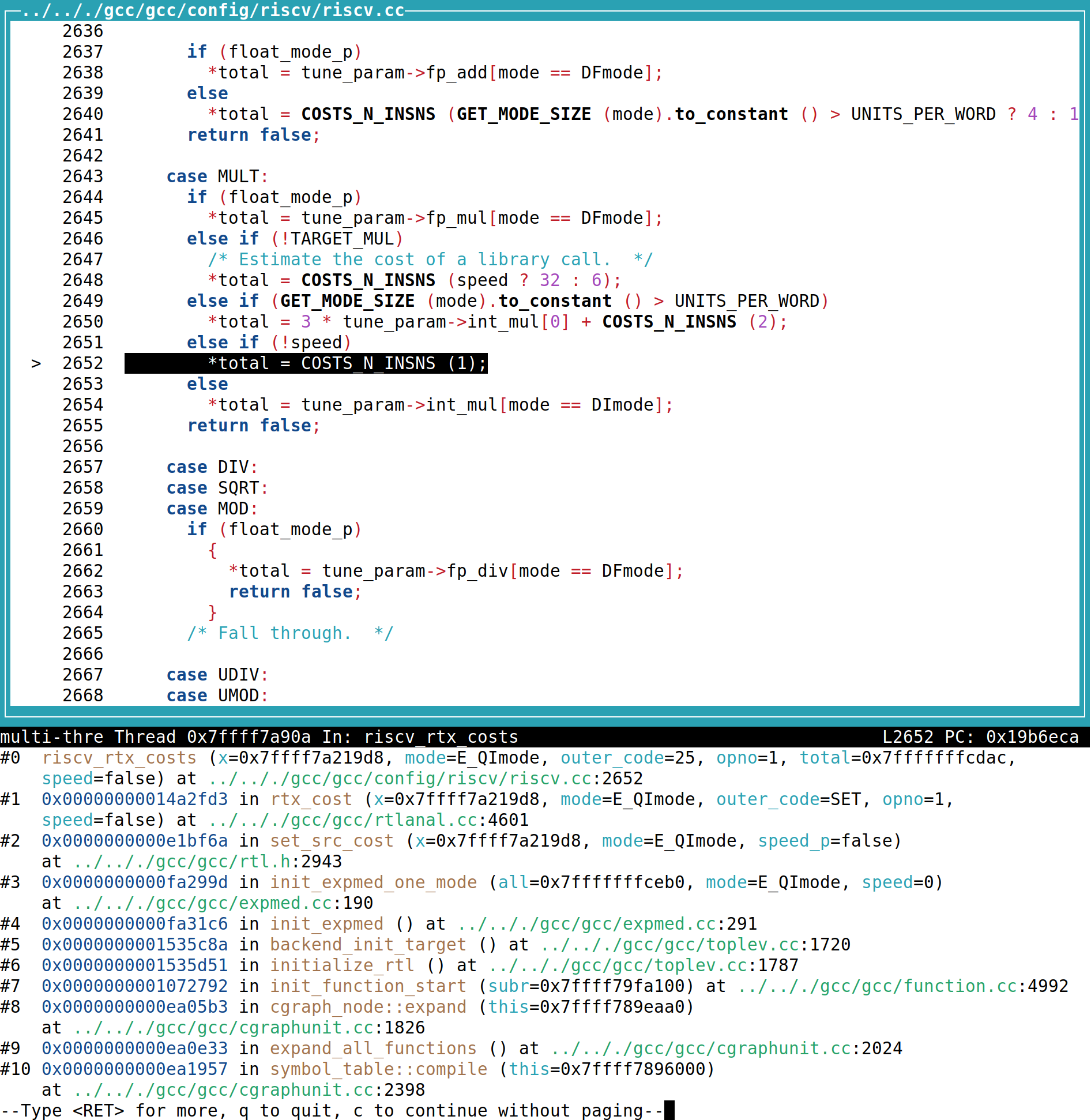
一直单步运行下去,直到找出最后影响costs的位置:
发现在 riscv/riscv.cc 中有一个名为riscv_rtx_costs的函数,继续观察发现,当speed=1时,选用的*total来源于tune_param。
我们接着观察tune_param的来源:
(gdb) p tune_param
$2 = (const riscv_tune_param *) 0x2a06b20 <rocket_tune_info>然后我们去找它的定义:
// File: gcc/config/riscv/riscv.cc
/* Costs to use when optimizing for rocket. */
static const struct riscv_tune_param rocket_tune_info = {
{COSTS_N_INSNS (4), COSTS_N_INSNS (5)}, /* fp_add */
{COSTS_N_INSNS (4), COSTS_N_INSNS (5)}, /* fp_mul */
{COSTS_N_INSNS (20), COSTS_N_INSNS (20)}, /* fp_div */
{COSTS_N_INSNS (4), COSTS_N_INSNS (4)}, /* int_mul */
{COSTS_N_INSNS (6), COSTS_N_INSNS (6)}, /* int_div */
1, /* issue_rate */
3, /* branch_cost */
5, /* memory_cost */
8, /* fmv_cost */
true, /* slow_unaligned_access */
};这里发现,上面的fp_add到int_div都有两项,通过观察使用它的代码发现,它的引用都是形如fp_add[mode == DFmode],int_mul[mode == DImode],int_div[mode == DImode]的形式。
而这些Mode又是什么呢?我又查阅了GCC文档。
BImode: “Bit” mode represents a single bit, for predicate registers.
SImode: “Single Integer” mode represents a four-byte integer.
DImode: “Double Integer” mode represents an eight-byte integer.原来只是不同的操作数长度和类型。
然后我们的重点就放到了cost上了。
首先观察div和mul的cost差距:
{COSTS_N_INSNS (4), COSTS_N_INSNS (4)}, /* int_mul */
{COSTS_N_INSNS (6), COSTS_N_INSNS (6)}, /* int_div */可以看到,这里假定了mul的cost是4,div的cost是6。
这个值是否合理呢?我们去看Rocket CPU里面乘除法器怎么写的。
Rocket CPU RTL观察
我们首先观察Rocket的乘除法器有哪些参数:
// File: rocket-chip/src/main/scala/rocket/Multiplier.scala
case class MulDivParams(
mulUnroll: Int = 1,
divUnroll: Int = 1,
mulEarlyOut: Boolean = false,
divEarlyOut: Boolean = false,
divEarlyOutGranularity: Int = 1
)然后,我们观察一下使用BigCores的情况下,它设置了什么参数:
// File: rocket-chip/src/main/scala/subsystem/Configs.scala
class WithNBigCores(
n: Int,
overrideIdOffset: Option[Int] = None,
crossing: RocketCrossingParams = RocketCrossingParams()
) extends Config((site, here, up) => {
case TilesLocated(InSubsystem) => {
val prev = up(TilesLocated(InSubsystem), site)
val idOffset = overrideIdOffset.getOrElse(prev.size)
val big = RocketTileParams(
core = RocketCoreParams(mulDiv = Some(MulDivParams(
mulUnroll = 8,
mulEarlyOut = true,
divEarlyOut = true))),
dcache = Some(DCacheParams(
rowBits = site(SystemBusKey).beatBits,
nMSHRs = 0,
blockBytes = site(CacheBlockBytes))),
icache = Some(ICacheParams(
rowBits = site(SystemBusKey).beatBits,
blockBytes = site(CacheBlockBytes))))
List.tabulate(n)(i => RocketTileAttachParams(
big.copy(hartId = i + idOffset),
crossing
)) ++ prev
}
})可以看到,就是将mulUnroll设置为了8,然后对于mul和div都开启EarlyOut。
那么,EarlyOut又是什么呢?我们观察除法器:
// File: rocket-chip/src/main/scala/rocket/Multiplier.scala
if (cfg.divEarlyOut) {
val align = 1 << log2Floor(cfg.divUnroll max cfg.divEarlyOutGranularity)
val alignMask = ~((align-1).U(log2Ceil(w).W))
val divisorMSB = Log2(divisor(w-1,0), w) & alignMask
val dividendMSB = Log2(remainder(w-1,0), w) | ~alignMask
val eOutPos = ~(dividendMSB - divisorMSB)
val eOut = count === 0.U && !divby0 && eOutPos >= align.U
when (eOut) {
remainder := remainder(w-1,0) << eOutPos
count := eOutPos >> log2Floor(cfg.divUnroll)
}
}我们可以看出,当还没被除的数已经小于了除数时,可以肯定后续的都不必继续除,而直接作为余数。因此我们可以看出,这样的除法的周期数是和其值的大小相关的。
而对于乘法也是同理:
if (cfg.mulUnroll != 0) when (state === s_mul) {
val mulReg = Cat(remainder(2*mulw+1,w+1),remainder(w-1,0))
val mplierSign = remainder(w)
val mplier = mulReg(mulw-1,0)
val accum = mulReg(2*mulw,mulw).asSInt
val mpcand = divisor.asSInt
val prod = Cat(mplierSign, mplier(cfg.mulUnroll-1, 0)).asSInt * mpcand + accum
val nextMulReg = Cat(prod, mplier(mulw-1, cfg.mulUnroll))
val nextMplierSign = count === (mulw/cfg.mulUnroll-2).U && neg_out
val eOutMask = ((BigInt(-1) << mulw).S >> (count * cfg.mulUnroll.U)(log2Up(mulw)-1,0))(mulw-1,0)
val eOut = (cfg.mulEarlyOut).B && count =/= (mulw/cfg.mulUnroll-1).U && count =/= 0.U &&
!isHi && (mplier & ~eOutMask) === 0.U
val eOutRes = (mulReg >> (mulw.U - count * cfg.mulUnroll.U)(log2Up(mulw)-1,0))
val nextMulReg1 = Cat(nextMulReg(2*mulw,mulw), Mux(eOut, eOutRes, nextMulReg)(mulw-1,0))
remainder := Cat(nextMulReg1 >> w, nextMplierSign, nextMulReg1(w-1,0))
count := count + 1.U
when (eOut || count === (mulw/cfg.mulUnroll-1).U) {
state := s_done_mul
resHi := isHi
}
}同时我们也可以看出,在操作数足够小时,Rocket上乘法器最小输出是2个周期,除法器最小输出是3个周期,但假设按照大核的默认配置,即乘法做8宽度的Unroll,除法不做Unroll,乘法的最大延迟是8个周期,但除法会达到惊人的64+1=65周期。
那么问题来了,Rocket大核配置上这种情况到底哪个快呢?
我们使用以下代码进行测试:
int main() {
int x = 0;
for (int i=0;i<1000;i++) x ^= i / 6;
return x;
}我们观察两份编译产物:
第一份是使用divw:
000000002000004c <main>:
2000004c: 4781 li a5,0
2000004e: 4501 li a0,0
20000050: 4619 li a2,6
20000052: 3e800693 li a3,1000
20000056: 02c7c73b divw a4,a5,a2
2000005a: 2785 addw a5,a5,1
2000005c: 8d39 xor a0,a0,a4
2000005e: 2501 sext.w a0,a0
20000060: fed79be3 bne a5,a3,20000056 <main+0xa>
20000064: 8082 ret第二份则是修改了GCC的expmed cost,将div cost由6改为8,这样遇到该除法可以换成Barrett reduction:
000000002000004c <main>:
2000004c: 2aaab637 lui a2,0x2aaab
20000050: 4701 li a4,0
20000052: 4501 li a0,0
20000054: aab60613 add a2,a2,-1365 # 2aaaaaab <bootstacktop+0xaaaa60b>
20000058: 3e800593 li a1,1000
2000005c: 02c707b3 mul a5,a4,a2
20000060: 41f7569b sraw a3,a4,0x1f
20000064: 2705 addw a4,a4,1
20000066: 9381 srl a5,a5,0x20
20000068: 9f95 subw a5,a5,a3
2000006a: 8d3d xor a0,a0,a5
2000006c: 2501 sext.w a0,a0
2000006e: feb717e3 bne a4,a1,2000005c <main+0x10>
20000072: 8082 ret我们来直接用Verilator跑RTL代码看看:
第一份代码(直接使用divw):
➜ emulator git:(soc) ✗ ./obj_dir/VTestHarness 2>&1 | grep "pc=\[000000002000004a\]" | head -n 1
C0: 19551 [1] pc=[000000002000004a] W[r 0=000000002000004c][1] R[r 0=0000000000000000] R[r 0=0000000000000000] inst=[0000a001] DASM(0000a001)耗时19551个Cycle
第二份代码(优化为Barrett reduction):
➜ emulator git:(soc) ✗ ./obj_dir/VTestHarness 2>&1 | grep "pc=\[000000002000004a\]" | head -n 1
C0: 15342 [1] pc=[000000002000004a] W[r 0=000000002000004c][1] R[r 0=0000000000000000] R[r 0=0000000000000000] inst=[0000a001] DASM(0000a001)比刚才少了4000多个cycle。
可以看出,即使非常小的数的乘法,将除法替换为Barrett reduction也能获得更快的结果。
最后放上一张Rocket使用不同参数的性能测试结果:
| mul unroll | mul cycles | Div unroll | div cycles |
|---|---|---|---|
| 1 | 21326 | 1 | 19551 |
| 2 | 17022 | 2 | 16103 |
| 4 | 15342 | 4 | 15047 |
| 8 | 15342 | 8 | 14063 |
| 16 | 15342 | 16 | 13319 |
| 32 | 15342 | 32 | 13319 |
然而,对于一般CPU核心来说,div的延迟远高于mul,如果我们配置大量的div unroll通常达不到预期的CPU频率。根据 uops.info 上的数据,按照x86 CPU执行32位寄存器乘法,AMD Zen4与Intel Alderlake大概都是3-4个Cycle,而对于32位寄存器除法 则需要10个Cycle以上。
因此,我怀疑GCC的RISC-V里对于Rocket的Tune数据全按照最低Cycle数量 *2 计算,在性能上是有些问题的。
TH1520性能测试
我还使用了采用C910处理器的TH1520 SoC进行测试。
int main() {
int x = 0;
int loop = 1e8;
for (int i=0;i<loop;i++) x ^= i / 6;
return x;
}分别得到:
使用Barrett reduction优化的代码:
.file "1.c"
.option nopic
.attribute arch, "rv64i2p1_m2p0_a2p1_f2p2_d2p2_c2p0_zicsr2p0"
.attribute unaligned_access, 0
.attribute stack_align, 16
.text
.section .text.startup,"ax",@progbits
.align 1
.globl main
.type main, @function
main:
.LFB0:
.cfi_startproc
li a1,715829248
li a2,99999744
li a4,0
li a0,0
addi a1,a1,-1365
addi a2,a2,256
.L2:
mul a5,a4,a1
sraiw a3,a4,31
addiw a4,a4,1
srli a5,a5,32
subw a5,a5,a3
xor a0,a0,a5
sext.w a0,a0
bne a4,a2,.L2
ret
.cfi_endproc
.LFE0:
.size main, .-main
.ident "GCC: (GNU) 13.2.1 20230801"
.section .note.GNU-stack,"",@progbits直接除法的代码:
.file "1.c"
.option nopic
.attribute arch, "rv64i2p1_m2p0_a2p1_f2p2_d2p2_c2p0_zicsr2p0"
.attribute unaligned_access, 0
.attribute stack_align, 16
.text
.section .text.startup,"ax",@progbits
.align 1
.globl main
.type main, @function
main:
.LFB0:
.cfi_startproc
li a3,99999744
li a5,0
addi a3,a3,256
li a0,0
li a2,6
.L2:
divw a4,a5,a2
addiw a5,a5,1
xor a0,a0,a4
sext.w a0,a0
bne a5,a3,.L2
ret
.cfi_endproc
.LFE0:
.size main, .-main
.ident "GCC: (GNU) 13.2.1 20230801"
.section .note.GNU-stack,"",@progbits性能如下:
➜ div_perf time ./mul
./mul 0.24s user 0.00s system 99% cpu 0.248 total
➜ div_perf time ./div
./div 0.64s user 0.00s system 99% cpu 0.640 total可以看出,同样也是把常数除法改Barrett reduction性能更好。
JH7110性能测试
使用VisionFive 2进行,与TH1520同样的方法:
➜ div_perf time ./div
./div 1.98s user 0.00s system 99% cpu 1.981 total
➜ div_perf time ./mul
./mul 0.40s user 0.00s system 99% cpu 0.403 total在这里,使用Barrett reduction替换后远比除法快。
后续
已将Patch提交给上游并合并入GCC主线。