HDU 6657 – Acesrc and Cube Hypernet
Table of Contents
题意:
给一个纸条,问是否可以折成一个立方体,纸条用一个h*w的矩阵上的#来描述,h<=100,w<=100,T<=30(数据组数)。
分析:
当时多校赛场上读完题就想到了可以枚举点然后BFS填充格子,只要有一个起点能满足不重复地填充给出图形上的所有#号点,且立方体被填满,就输出yes。由于h<=100,w<=100,所以最大的正方体的边长为100/4=25,因此我们枚举点25*25,check使用25*25*6的复杂度可以完成。
不过因为后来跟榜先搞别的题去了这题就先放一边,结果我们队后来因为开车那题自闭到最后.
这题的难点在于处理BFS时转向的问题。
我们可以先建立一个三维坐标,第一维是所属的面,第二维和第三维是这个坐标在这个面中的位置。如下图所示,中间的数字是面坐标的编号。
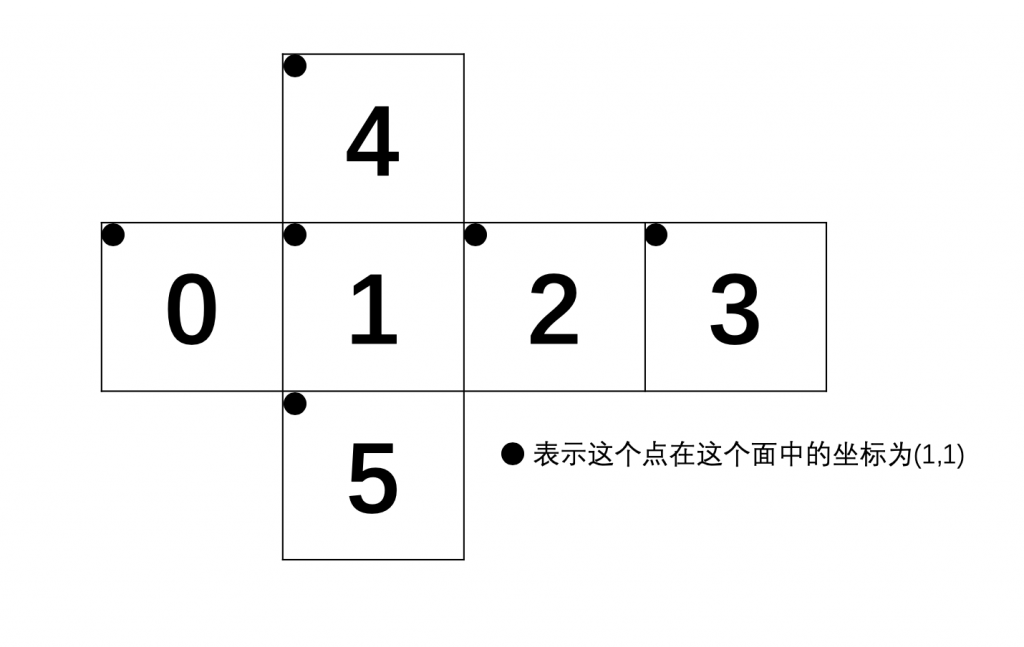
然后对于编号1的面,向周围4个面走的时候都是直接走即可,不需要进行坐标变换。
而对于需要进行坐标变换的情况,比如从0这个面一直向上走,走到4,需要将x和y坐标对调,然后逆时针转90°,再继续填充这个格子。
对于6个面,向4个方向走只有6*4=24种情况,所以直接把这24种情况x和y和方向的变化写出来(可以用if或者switch),然后直接做就完了。
然后就直接上一段很丑的代码吧。(为什么这么丑还要写博客呢,因为这算是在多校期间补的题中AC的人最少的一道题吧)
代码:
#include <bits/stdc++.h>
using namespace std;
int sz;
int trans(int &x,int &y,int °,int from) {//x和y是这个点在该面的坐标,from是当前面的编号,返回移动之后面的编号
if (from == 0) {
if (y == sz + 1) {
y = 1;
return 1;
}
else if (y == 0) {
y = sz;
return 3;
}
else if (x == 0) {
x = y;
y = 1;
deg = (deg - 1 + 4) % 4;
return 5;
}
else if (x == sz + 1) {
x = sz - y + 1;
y = 1;
deg = (deg + 1 + 4) % 4;
return 4;
}
}
else if (from == 1) {
if (x == 0) {
x = sz;
return 5;
}
else if (x == sz + 1) {
x = 1;
return 4;
}
else if (y == 0) {
y = sz;
return 0;
}
else if (y == sz + 1) {
y = 1;
return 2;
}
}
else if (from == 2) {
if (y == 0) {
y = sz;
return 1;
}
else if (y == sz + 1) {
y = 1;
return 3;
}
else if (x == 0) {
x = sz - y + 1;
y = sz;
deg = (deg + 1 + 4) % 4;
return 5;
}
else if (x == sz + 1) {
x = y;
y = sz;
deg = (deg - 1 + 4) % 4;
return 4;
}
}
else if (from == 3) {
if (y == 0) {
y = sz;
return 2;
}
else if (y == sz + 1) {
y = 1;
return 0;
}
else if (x == 0) {
y = sz + 1 - y;
x = 1;
deg = (deg + 2 + 4) % 4;
return 5;
}
else if (x == sz + 1) {
y = sz + 1 - y;
x = sz;
deg = (deg - 2 + 4) % 4;
return 4;
}
}
else if (from == 4) {
if (x == 0) {
x = sz;
return 1;
}
else if (x == sz + 1) {
x = sz;
y = sz + 1 - y;
deg = (deg + 2 + 4) % 4;
return 3;
}
else if (y == 0) {
y = sz - x + 1;
x = sz;
deg = (deg - 1 + 4) % 4;
return 0;
}
else if (y == sz + 1) {
y = x;
x = sz;
deg = (deg + 1 + 4) % 4;
return 2;
}
}
else if (from == 5) {
if (x == sz + 1) {
x = 1;
return 1;
}
else if (x == 0) {
x = 1;
y = sz - y + 1;
deg = (deg - 2 + 4) % 4;
return 3;
}
else if (y == 0) {
y = x;
x = 1;
deg = (deg + 1 + 4) % 4;
return 0;
}
else if (y == sz + 1) {
y = sz - x + 1;
x = 1;
deg = (deg - 1 + 4) % 4;
return 2;
}
}
return -1;
}
const int dx[4] = {1,0,-1,0};
const int dy[4] = {0,1,0,-1};
char s[105][105];
bool vis[105][105];
bool vis2[6][105][105];
int h,w,si,sj;
struct DATA {
int i,j,x,y,z,dir;
};
bool check(int x,int y) {
memset(vis,0,sizeof(vis));
memset(vis2,0,sizeof(vis2));
vis[si][sj] = true;
queue <DATA> q;
q.push({si,sj,x,y,0,0});
vis2[0][x][y] = true;
int cnt = 0;
while (!q.empty()) {
auto cur = q.front();
q.pop();
cnt ++;
for (int d=0;d<4;d++) {
int ni = cur.i + dx[d];
int nj = cur.j + dy[d];
if (ni < 1 || nj < 1 || ni > h || nj > w || s[ni][nj] != '#' || vis[ni][nj]) continue;
vis[ni][nj] = true;
int nx = cur.x + dx[(d+cur.dir)%4];
int ny = cur.y + dy[(d+cur.dir)%4];
int nz = cur.z;
int ndir = cur.dir;
if (nx == 0 || ny == 0 || nx == sz + 1 || ny == sz + 1) nz = trans(nx,ny,ndir,cur.z);
if (vis2[nz][nx][ny]) continue;
vis2[nz][nx][ny] = true;
q.push({ni,nj,nx,ny,nz,ndir});
}
}
return cnt == sz * sz * 6;
}
int main() {
int T;
scanf("%d",&T);
while (T --) {
scanf("%d%d",&h,&w);
int cnt = 0;
for (int i=1;i<=h;i++) {
scanf("%s",&s[i][1]);
for (int j=1;j<=w;j++) {
if (s[i][j] == '#') {
cnt ++;
si = i;
sj = j;
}
}
}
sz = sqrt(cnt / 6) + 0.5;
if (sz * sz * 6 == cnt) {
bool ans = false;
for (int i=1;i<=sz && !ans;i++) for (int j=1;j<=sz && !ans;j++) {
if (check(i,j)) ans = true;
}
if (ans) printf("yes\n");
else printf("no\n");
}
else printf("no\n");
}
return 0;
}
cyy大神太强了呀。orz
cyynb
cyytql
King of ICPC
cyy太强了啊